r(t) = a₀ + a₁t + a₂ sin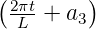

Model

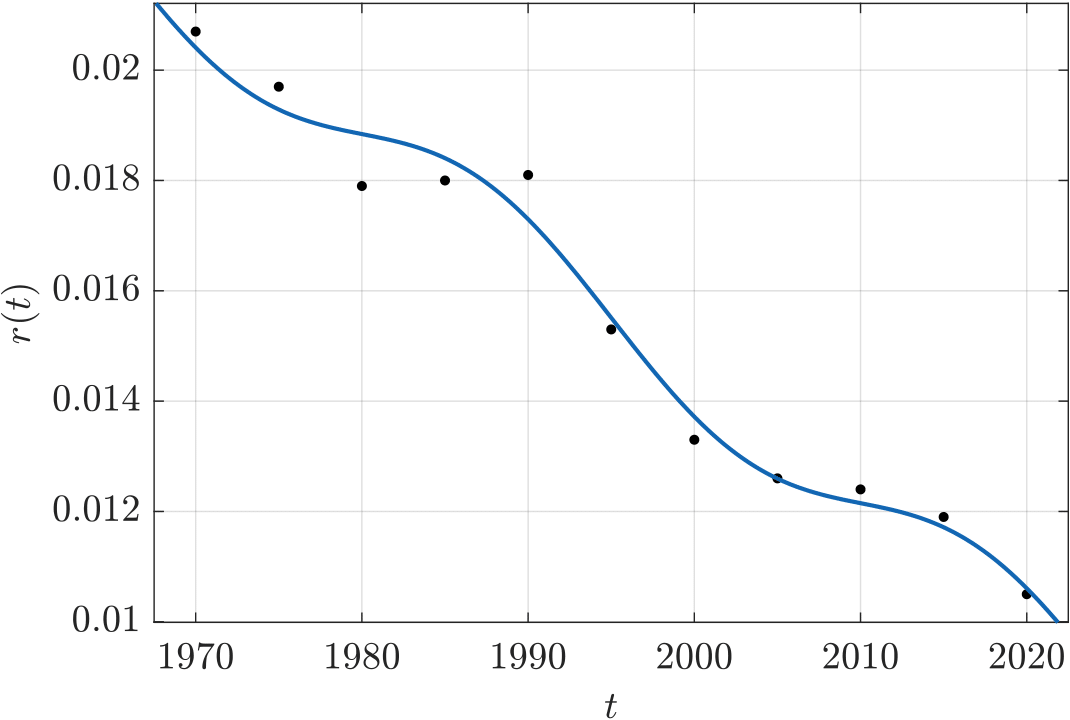
V případě, že se data pokusíme proložit zmíněnou nelineární regresní křivkou s harmonickou složkou, nabude model tvaru

Odhad parametrů a₀, a₁, a₂, a₃

Za využití metody nejmenších čtverců získáme pro dané parametry hodnoty

• a₀ = 0.460459,
• a₁ = −0.000223,
• a₂ = 0.0007788,
• a₃ = −0.00108.

Hodnota parametru a₃ není ve skutečnosti statisticky významná, dále jej tedy nebudeme uvažovat, tj. a₃ := 0. Příslušné proložení je znázorněno na obrázku 5.

---

---

Výsledná predikce

Po dosazení vypočtených parametrů získáme predikci

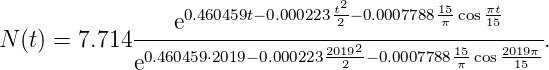(3)

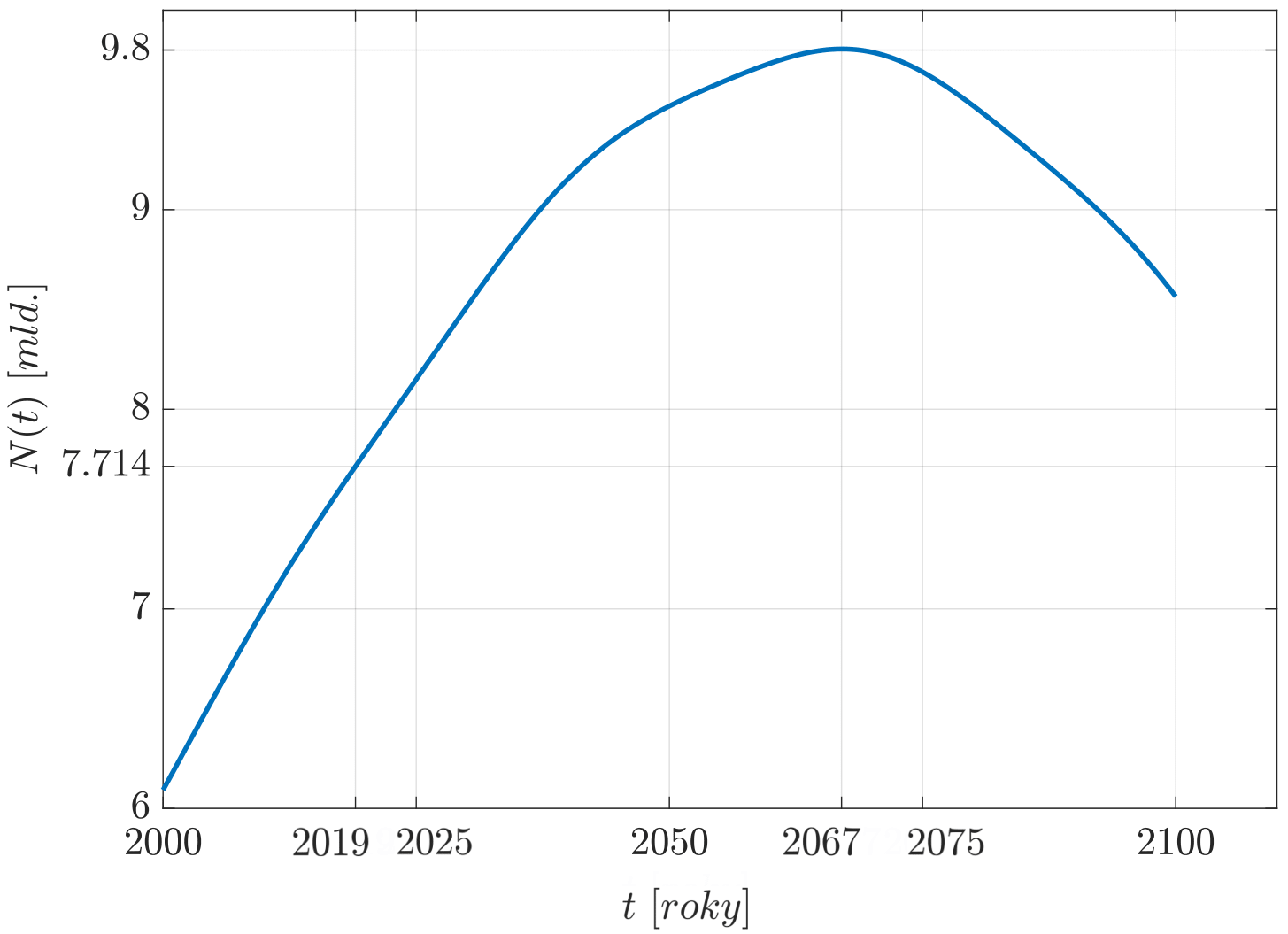
Příslušný vývoj velikosti lidské populace je zobrazen v grafu 6. Na základě modelu (3) tak můžeme předpovědět, že lidská populace dosáhne svého maxima kolem roku 2067 (cca 9.8 mld. obyvatel) a následně začne klesat. Můžeme si povšimnout, že daná předpověď je velice podobná té v předchozím případě. Nakonec poznamenejme, že jsou oba modely velice citlivé na změny svých parametrů, což bychom měli brát v úvahu zvláště při jejich interpretaci.

---

---