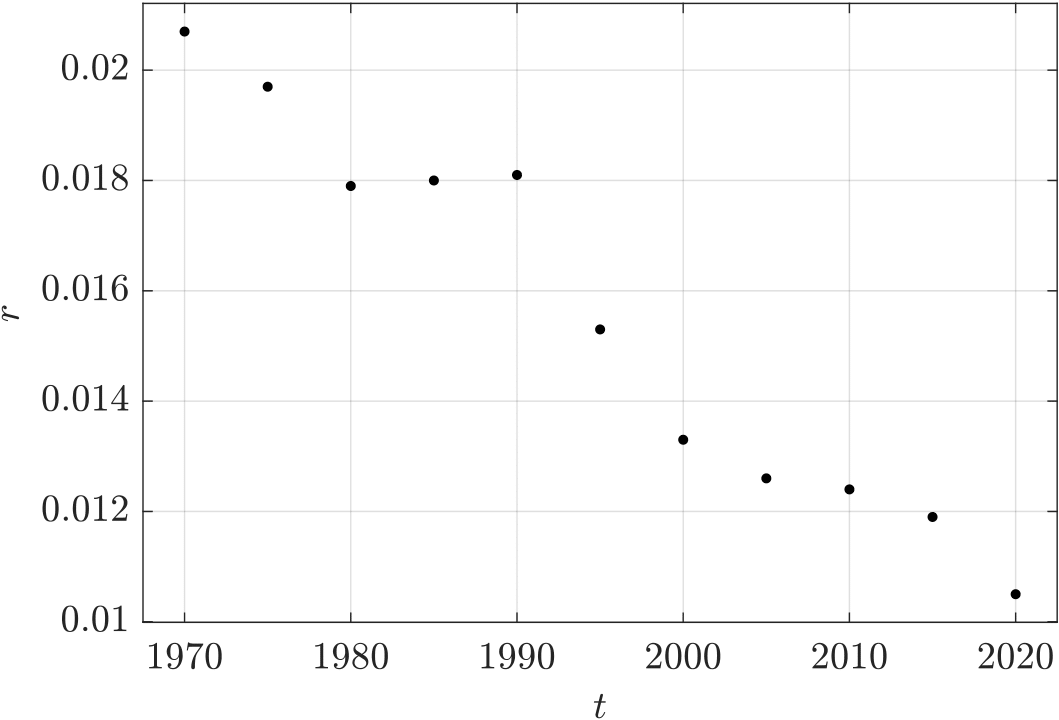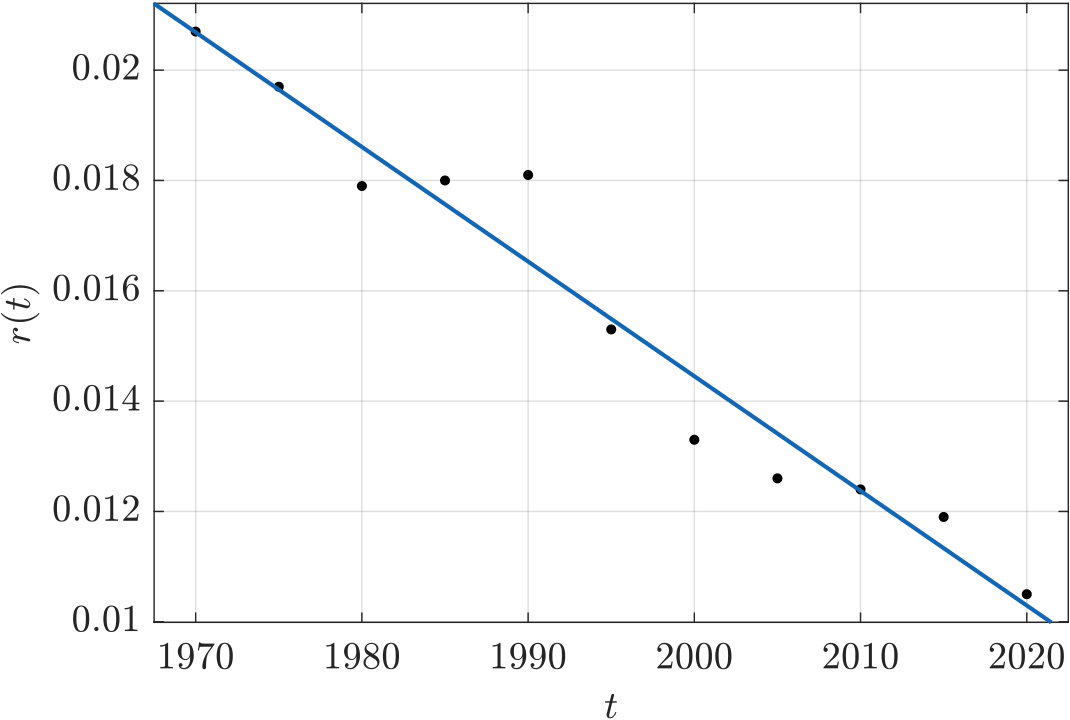Model populace planety

Následující model
2019

Počet lidí na Zemi

Odvození obecného modelu

Označme N(t) velikost lidské populace v čase t. Dále nechť r(t) představuje míru růstu této populace (procentuální nárůst počtu obyvatel) v čase t. Velikost populace v čase t + Δt pak můžeme vyjádřit rovnicí

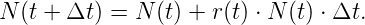
N (t + Δt ) = N (t) + r(t) ⋅ N (t) ⋅ Δt.

Tento vztah upravíme do tvaru

N (t + Δt ) − N (t) ------------------= r(t) ⋅ N (t) Δt

a limitním přechodem Δt → 0 obdržíme výslednou diferenciální rovnici
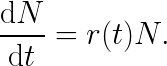dN ----= r(t)N, dt
(1)

Pro zjednodušení zápisu zde zanedbáváme časový argument funkce N(t). Míra růstu r(t) je neznámá funkce v proměnné t, kterou odhadneme s využitím tzv. lineární a nelineární regrese. Příslušná data jsou zobrazena v následující tabulce a na obrázku 2. Jejich zdrojem je https://www.worldometers.info/world-population.

r00.02070.01970.01790.01800.01810.01530.01330.01260.01240.01190.0105
rok 1970 1975 1980 1985 1990 1995 2000 2005 2010 2015 2020

PIC

Pro prokládanou funkci r(t) budeme uvažovat následující varianty:

(a)
r(t) = a0 + a1t,
(b)
r(t) = a0 + a1t + a2 sin 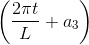(2πt) L, kde L ≈ 30 značí průměrný věk matky při narození některého z potomků.

Řešením rovnice (1) je (2πt)L

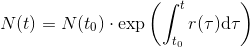
Za počátek t0 budeme předpokládat současnost, tzn. rok t0 = 2019, kdy je na Zemi cca 7.714 mld. obyvatel, tj. N(2019) = 7.714 [mld.].

r(t) = a0 + a1t

Model

V případě, že data proložíme prostou regresní přímkou, nabude model tvaru

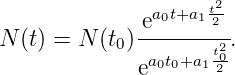
2 ea0t+a1t2- N (t) = N (t0)-------t2. ea0t0+a120

Odhad parametrů a0 a a1

Za využití metody nejmenších čtverců získáme pro dané parametry hodnoty

Uvažované proložení je znázorněno na obrázku 3.

PIC

Výsledná predikce

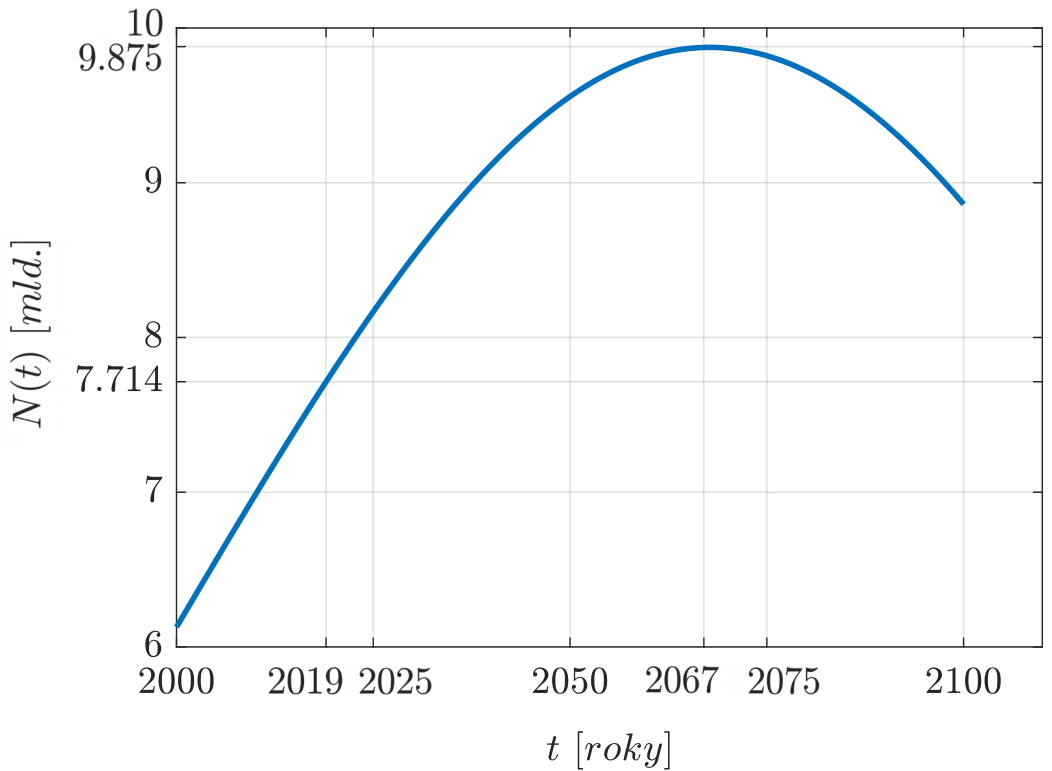
Po dosazení vypočtených parametrů obdržíme výslednou predikci
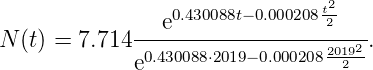e0.430088t− 0.000208t22 N (t) = 7.714 ------------------20192. e0.430088⋅2019−0.000208--2-
(2)

Příslušný vývoj velikosti lidské populace je zobrazen v grafu 4. Na základě modelu (2) tak můžeme předpovědět, že lidská populace dosáhne svého maxima kolem roku 2067 (cca 9.875 mld. obyvatel) a následně začne klesat.