Populační model

V modelu bude symbol N(t) značit velikost lidské populace v čase t. Budeme používat model, ve kterém bude koeficient růstu vyjádřen jako funkce závislá na velikosti populace: r(N). Rovnici našeho modelu ve spojitém případě tedy můžeme zapsat jako:

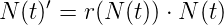
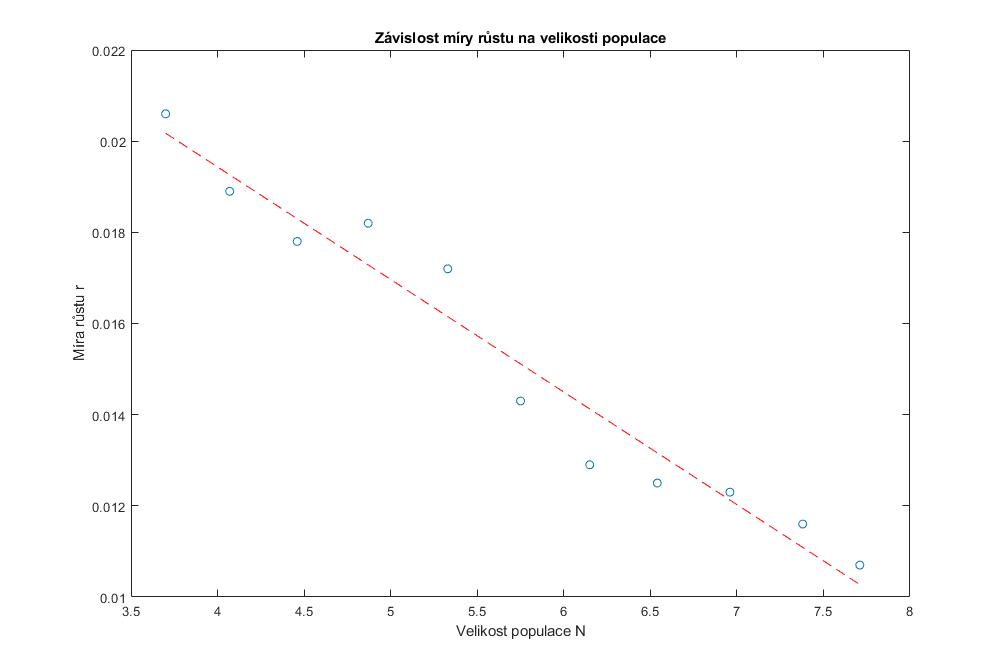
Funkci koeficientu růstu r(N) budeme muset odhadnout pomocí lineární regrese. Vycházet budeme z dat od roku 1970 do součastnosti dostupných na https://www.worldometers.info/world-population.

Funkci r(N) se pokusíme vyjádřit jako lineární závislost:

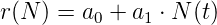
Za počátek t₀ zvolíme rok 1970, tzn. rok t₀ = 1970, tedy rok, od kterého naše data počítáme, přičemž: N(1970) = 3.7 [mld.].

Metodou nejmenších čtverců získáme odhat pro koeficienty a₀ a a₁ :

• a₀ = 0.02931,
• a₁ = −0.002469.

Po dosazení r(N) do rovnice modelu a vyjádřením funkce N(t) (vypočtením příslušné diferenciální rovnice), získáme:

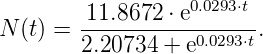(1)

Podle grafu funkce velikosti lidské populace N(t) můžeme usoudit, že lidská populace bude dále růst, ale tento růst se bude zpomalovat. Do roku 2170 by lidská populace měla konvergovat k 11.8 miliardám.

Model nebude nikdy klesající, neboť jsme zvolili klesající funkci r(N) (přímku) - čím větší tedy populace bude, tím pomaleji bude růst. A čím menší bude koeficient růstu, tím menší bude růst populace - růst bude tedy stále pomalejší, ale nikdy se úplně nezastaví. Takovýto model můžeme použít např. na aproximaci kapacity prostředí, v našem případě kolem 11.8 mld. lidí.