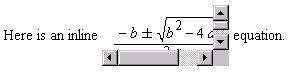
Scripting the techexplorer Hypermedia Browser

Automatically Sizing Embedded techexplorer Windows in HTML

When using the <OBJECT> tag to invoke the ActiveX control version of techexplorer, the AutoSize parameter can be used to size an embedded techexplorer window automatically. However, when using the <EMBED> tag to include a reference to the techexplorer plug-in, the window size (width and height) must be fixed. This can be a problem when mixing-n-matching techexplorer equations and HTML constructs. Indeed, it is silly always to expect the author or the application that created the markup for the embedded object to know ahead of time how big an equation will be when rendered. Equation composition consists of non-trivial computations and is very dependent on the fonts used and their sizes. Knowing the width, height and depth can be the difference between a web page that looks like this:

vs. one that looks like this:

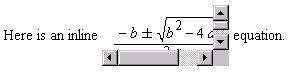
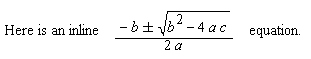
It is the renderer of the markup and not the producer that should compute the correct height, depth, and width of the object. By using the techexplorer Java API and JavaScript code this situation can be palliated. Users can now create web pages that automatically determine the alignment and correct size of techexplorer rendered mathematical equations. The techexplorerPlugin Java class provides seven methods for determining the width, height and depth of a LaTeX and MathML expression: getWidthFromMMLString(String mmlSource), getHeightFromMMLString(String mmlSource), getDepthFromMMLString(String mmlSource), getWidthFromTeXString(String texSource), getHeightFromTeXString(String texSource), getHeightFromTeXStringAndWidth(String texSource, int width), and getDepthFromTeXString(String texSource).

Automatically Sizing Mathematical Expressions

The following HTML source shows how to use the techexplorer JavaScript Library (techexplorer.js) to generate a HTML document dynamically that contains correctly sized techexplorer mathematical expressions for both Netscape and Internet Explorer!

<HTML>
<BODY>
<OBJECT ID="techexplorer" HEIGHT=3 WIDTH=3
    CLASSID="clsid:5AFAB315-AD87-11D3-98BB-002035EFB1A4">
    <PARAM NAME="DataType" VALUE="0">
    <PARAM NAME="Data" VALUE="">
    <EMBED TYPE="application/x-techexplorer"
        TEXDATA=""       
        HEIGHT=3 WIDTH=3 NAME="techexplorer">
    </EMBED>           
</OBJECT>
<SCRIPT TYPE="text/javascript" SRC="../Scripting/techexplorer.js"></SCRIPT>
Here is an inline 
<SCRIPT>displayAutosizeLaTeX(document.techexplorer, "$\\frac{-b\\pm\\sqrt{b^{2} - 4 \\, a \\,c } } {2 \\, a}$", 200, 100 )</SCRIPT>
equation.
</HTML>
</BODY>

Use the "options" menu to increase the techexplorer font size. Netscape users can hit the reload button in your web browser to see the JavaScript code automatically adjust each techexplorer window's width and height!

Automatically Sizing LaTeX Documents

The following JavaScript source shows how the techexplorer JavaScript Library (techexplorer.js) uses getHeightFromTeXStringAndWidth to generate a HTML document dynamically that contains correctly sized techexplorer LaTeX document fragments!

<SCRIPT LANGUAGE="JavaScript">
<HTML>
<BODY>
<OBJECT ID="techexplorer" HEIGHT=3 WIDTH=3
    CLASSID="clsid:5AFAB315-AD87-11D3-98BB-002035EFB1A4">
    <PARAM NAME="DataType" VALUE="0">
    <PARAM NAME="Data" VALUE="">
    <EMBED TYPE="application/x-techexplorer"
        TEXDATA=""       
        HEIGHT=3 WIDTH=3 NAME="techexplorer">
    </EMBED>           
</OBJECT>
<SCRIPT TYPE="text/javascript" SRC="../Scripting/techexplorer.js"></SCRIPT>
<SCRIPT>
displayLaTeXWithFixedWidth(document.techexplorer,
	"\\section{Square--Free Decomposition} \
	In this paper we deal with problem of the computation of the square--free \
	decomposition of $f \\in K[x]$, a univariate \
	polynomial with coefficients in a field $K$ of positive characteristic. \
	We say that $f$ is {\\bf square--free} over $K$ if whenever $g \\in K[x]$ \
	is such that $g^2 | f$ then $g \\in K$. \
	We say that polynomials \
	$P_1,\\ldots, P_s$ give a {\\bf square--free decomposition} of $f$ if: \
	\\begin{itemize} \
	\\item $f = \\prod {P_i}^i$ \
	\\item {\\rm gcd}$(P_i,P_j) = 1$, if  $i \\neq j$ \
	\\item $P_i $ is square free for all $i$. \
	\\end{itemize} \
	There are known algorithms for the square--free decomposition of \
	polynomials with coefficients in a field of characteristic zero: in \
	[Y] there are the descriptions of three algorithms due to \
	Tobey--Horowitz, Musser and Yun respectively, for the computation of \
	square--free decomposition of univariate polynomials with rational \
	coefficients; actually, these algorithms \
	will  work over any computable field of characteristic zero."
	,500 , 500, "", "")
</SCRIPT>
</HTML>
</BODY>

Use the "options" menu to increase the techexplorer font size. Hit the reload button in your web browser to see the JavaScript code automatically adjust the techexplorer window height!

IBM techexplorer Hypermedia Browser is a trademark of the IBM Corporation.
Send comments and questions to techexpl@us.ibm.com.
Visit the official techexplorer home page at http://www.software.ibm.com/techexplorer/.