Priklad 12
V tomto prikladu se budeme se podrobneji zabyvat rovnici linearniho oscilatoru, coz je rovnice 2. radu tvaru
y''
+ 2
ay'
+
![]() y
= 0, kde
y
= 0, kde
![]() .
.
> restart;
> rovnice:=diff(y(x),x$2)+2*a*diff(y(x),x)+b^2*y(x)=0;
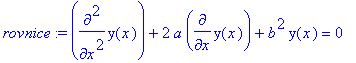
Urcime charakteristickou rovnici a vypocteme jeji koreny.
> read "difproc.m": char_rovnice:=char(rovnice,y(x));
![]()
> solve(char_rovnice,lambda);
![]()
Nyni provedeme diskuzi reseni v zavislosti na parametrech a , b .
I. Jestlize a=0 , je dana rovnice tvaru
> rovnice1:=subs(a=0,rovnice);
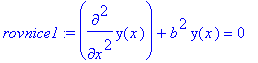
Urcime koreny charakteristicke rovnice a obecne reseni.
> solve(char(rovnice1,y(x)),lambda);
![]()
> ob_reseni1:=y(x)=c[1]*cos(b*x)+c[2]*sin(b*x);
![]()
Vzorec obecneho reseni lze upravit na vhodnejsi tvar, kde A > 0. Jedna se o tzv. harmonicke kmity .
> harmonicke:=y(x)=A*sin(b*x+phi);
![]()
Budeme uvazovat tyto zakladni hodnoty parametru:
A
= 1,
b
= 1,
![]() = 0. Budeme postupne animovat reseni tak, ze jeden z parametru budeme menit ve vhodnem rozsahu. Pri zmene parametru
A
bude dochazet ke zmene
amlitudy kmitani
, pri zmene parametru
b
dojde ke zmene
frekvence kmitani
(resp.
periody
) a pri zmene parametru
= 0. Budeme postupne animovat reseni tak, ze jeden z parametru budeme menit ve vhodnem rozsahu. Pri zmene parametru
A
bude dochazet ke zmene
amlitudy kmitani
, pri zmene parametru
b
dojde ke zmene
frekvence kmitani
(resp.
periody
) a pri zmene parametru
![]() dojde ke zmene
faze kmitani
.
dojde ke zmene
faze kmitani
.
> with(plots): animate(subs(b=1,phi=0,rhs(harmonicke)),x=-1.5..11,A=.5..4,scaling=constrained,view=[-1.5..11,-4..4],thickness=2,tickmarks=[6,4]); #amplituda
Warning, the name changecoords has been redefined
![[Maple Plot]](images/kmitani12.gif)
> animate(subs(A=1,phi=0,rhs(harmonicke)),x=-1.5..11,b=-3..3,scaling=constrained,view=[-1.5..11,-4..4],thickness=2,frames=90,numpoints=100,tickmarks=[6,4]); #frekvence
![[Maple Plot]](images/kmitani13.gif)
> animate(subs(A=1,b=1,rhs(harmonicke)),x=-1.5..11,phi=-5*Pi..5*Pi,scaling=constrained,view=[-1.5..11,-4..4],thickness=2,tickmarks=[6,4],frames=80); #faze
![[Maple Plot]](images/kmitani14.gif)
II.
Je-li
![]() >
>
![]() , pak charakteristicka rovnice ma dva realne ruzne koreny (vyraz
, pak charakteristicka rovnice ma dva realne ruzne koreny (vyraz
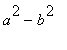 je totiz kladny). Kmitani, ktere je dano vzorcem obecneho reseni v tomto pripade, nazyvame
silne tlumene
.
je totiz kladny). Kmitani, ktere je dano vzorcem obecneho reseni v tomto pripade, nazyvame
silne tlumene
.
> silne:=y(x)=c[1]*exp((-a+sqrt(a^2-b^2))*x)+c[2]*exp((-a-sqrt(a^2-b^2))*x);
![silne := y(x) = c[1]*exp((-a+sqrt(a^2-b^2))*x)+c[2]...](images/kmitani18.gif)
Zobrazime graf reseni pro hodnoty konstant
![]() =
=
![]() = 1 a hodnoty parametru
a =
= 1 a hodnoty parametru
a =
![]() ,
b
= 1.
,
b
= 1.
> plot(subs(c[1]=1,c[2]=1,a=sqrt(2),b=1,rhs(silne)),x=-.5..4,y=0..3,thickness=2,scaling=constrained,tickmarks=[5,4]);
![[Maple Plot]](images/kmitani22.gif)
III.
Je-li
![]() , pak charakteristicka rovnice ma dvojnasobny realny koren
-a
. Jedna se o tzv.
kriticky tlumene kmity
.
, pak charakteristicka rovnice ma dvojnasobny realny koren
-a
. Jedna se o tzv.
kriticky tlumene kmity
.
> rovnice3:=subs(b^2=a^2,rovnice);
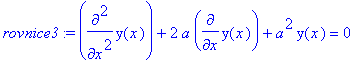
> solve(char(rovnice3,y(x)),lambda);
![]()
> kriticky:=y(x)=(c[1]+c[2]*x)*exp(-a*x);
![]()
Zobrazime graf reseni pro hodnoty konstant
![]() =
=
![]() = 1 a hodnotu parametru
a
= 1.
= 1 a hodnotu parametru
a
= 1.
> plot(subs(c[1]=1,c[2]=1,a=1,rhs(kriticky)),x=-1.5..3.8,y=-2..1.5,thickness=2,scaling=constrained,tickmarks=[5,4]);
![[Maple Plot]](images/kmitani29.gif)
IV.
Je-li
![]() <
<
![]() , ma charakteristicka rovnice dva komplexni sdruzene koreny (vyraz
, ma charakteristicka rovnice dva komplexni sdruzene koreny (vyraz
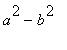 je totiz zaporny). Oznacime-li
je totiz zaporny). Oznacime-li
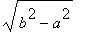 =
=
![]() > 0, pak obecne reseni je tvaru
> 0, pak obecne reseni je tvaru
> ob_reseni4:=y(x)=c[1]*exp(-a*x)*cos(omega*x)+c[2]*exp(-a*x)*sin(omega*x);
![]()
Obecne reseni je mozne upravit na nasledujici tvar.
> slabe:=y(x)=A*exp(-a*x)*sin(omega*x+phi);
![]()
Vezmeme za zakladni nasledujici hodnoty:
A
= 1,
a
= 1/3,
![]() = 4,
= 4,
![]() = 0. Obdobne jako v pripadu I., parametr
A
odpovida amplitude kmitani, parametr
= 0. Obdobne jako v pripadu I., parametr
A
odpovida amplitude kmitani, parametr
![]() udava jeho frekvenci a cislo
udava jeho frekvenci a cislo
![]() urcuje velikost fazoveho posuvu. Parametr
a
zde odpovida "rychlosti utlumu" kmitani.
urcuje velikost fazoveho posuvu. Parametr
a
zde odpovida "rychlosti utlumu" kmitani.
Nejprve si ukazeme, jak vypada graf reseni pro nami zvolene hodnoty. Graf reseni zobrazime spolu s "tlumici funkci", ktera ohranicuje krivku grafu. Tlumici funkci ziskame dosazenim maximalni hodnoty funkce sin(4 x ), tj. jednicky, do daneho reseni.
> dosazeni:=subs(A=1,a=1/3,omega=4,phi=0,rhs(slabe));
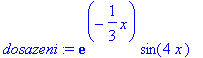
> tlum_fce:=exp(-1/3*x)*1;
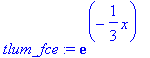
> graf:=plot(dosazeni,x=-3.3..5,color=red): tlum:=plot({tlum_fce,-tlum_fce},x=-3.3..5,color=black): display({graf,tlum},thickness=2,scaling=constrained,tickmarks=[4,3]);
![[Maple Plot]](images/kmitani43.gif)
Poznamka: Takto vytvorena "tlumici funkce" nespojuje presne body extremu daneho reseni (viz. zapisnik "tlumfce.mws").
Pomoci parametru A budeme menit amplitudu reseni spolu s jeho tlumici funkci. Vsimneme si, ze tlumici funkce je samozrejme take zavisla na hodnote parametru A .
> dosazeni1:=subs(a=1/3,omega=4,phi=0,rhs(slabe));
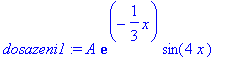
> tlum_fce1:=A*exp(-1/3*x);
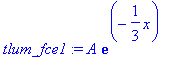
> ampl:=animate(dosazeni1,x=-3.3..5,A=.3..1,numpoints=100,color=red): tlum1:=animate({tlum_fce1,-tlum_fce1},x=-3.3..5,A=.3..1,color=black): display({tlum1,ampl},thickness=2,scaling=constrained,tickmarks=[4,3]); #amplituda
![[Maple Plot]](images/kmitani46.gif)
Dale budeme pomoci parametru a zrychlovat utlum reseni. Tlumici funkce je zavisla na velikosti parametru a . Pro hodnotu a = 0 se jedna o harmonicke kmity a tlumici funkce je konstantni.
> dosazeni2:=subs(A=1,omega=4,phi=0,rhs(slabe));
![]()
> tlum_fce2:=exp(-a*x);
![]()
> utlum:=animate(dosazeni2,x=-3.3..5,a=0..0.6,numpoints=100,color=red,frames=50): tlum2:=animate({tlum_fce2,-tlum_fce2},x=-3.3..5,a=0..0.6,color=black,frames=50): display({tlum2,utlum},view=[-3.3..5,-3..3],scaling=constrained,tickmarks=[4,3],thickness=2); #utlum
![[Maple Plot]](images/kmitani49.gif)
Pomoci parametru
![]() budeme zvetsovat frekvenci kmitani (resp. zmensovat periodu kmitani). Vsimneme si, ze tlumici funkce neni zavisla na velikosti parametru
budeme zvetsovat frekvenci kmitani (resp. zmensovat periodu kmitani). Vsimneme si, ze tlumici funkce neni zavisla na velikosti parametru
![]() , nemeni se (pokud zmenime pouze argument funkce sinus, jeji extremni hodnota se nezmeni) .
, nemeni se (pokud zmenime pouze argument funkce sinus, jeji extremni hodnota se nezmeni) .
> dosazeni3:=subs(A=1,a=1/3,phi=0,rhs(slabe));
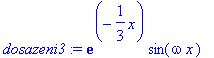
> tlum_fce3:=exp(-1/3*x)*1;
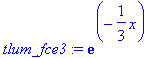
> frekvence:=animate(dosazeni3,x=-3.3..5,omega=0.2..5,numpoints=100,color=red,frames=60): tlum3:=plot({tlum_fce3,-tlum_fce3},x=-3.3..5,color=black): display({frekvence,tlum3},view=[-3.3..5,-3..3],scaling=constrained,tickmarks=[4,3],thickness=2); #frekvence
![[Maple Plot]](images/kmitani54.gif)
Zmenou parametru
![]() budeme menit fazi kmitani. Tlumici funkce neni na velikosti parametru
budeme menit fazi kmitani. Tlumici funkce neni na velikosti parametru
![]() zavisla.
zavisla.
> dosazeni4:=subs(A=1,a=1/3,omega=4,rhs(slabe));
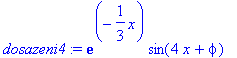
> tlum_fce4:=exp(-1/3*x)*1;
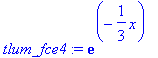
> posuv:=animate(dosazeni4,x=-3.3..5,phi=-5*Pi..5*Pi,numpoints=100,color=red,frames=50): display({posuv,tlum3},view=[-3.3..5,-3..3],scaling=constrained,tickmarks=[4,3],thickness=2); #fazovy posuv
![[Maple Plot]](images/kmitani59.gif)