Funkce v Maplu

> y:=x^2;

> subs(x=2,y);

Funkce muze byt zadana pomoci operatoru -> nebo jako procedura.

> y:=x->x^2;

> whattype(eval(y));

> whattype(y);

Vsimnete si rozdilu mezi:

> print(y);

> print(y(x));

> y(0);y(1);y(2);y(c);

> y;

> eval(y);

Zde se vyhodnocuje pouze jmeno funkce.

> y(t);

Vsimnete si rozdilu mezi predchazejicim zadanim a nasledujicimi prikazy:

> restart;

> y(x):=x^2;

> y(x), y(0), y(1/c);

> print(y);

Definovali jsme funkci, ale bez funkcniho predpisu.

> y:=x->x^2;

> print(y);

> infolevel[solve]:=1;

> solve(y=9,x);

solve:   Warning: no solutions found

> solve(y(x)=9,x);

Definovani funkce vice promennych:

> f:=(x,y)->x^3-3*x*y^2;

> f(3,2);

> plot3d(f,-1..1,-1..1,numpoints=2500, style=patchcontour, axes=framed);

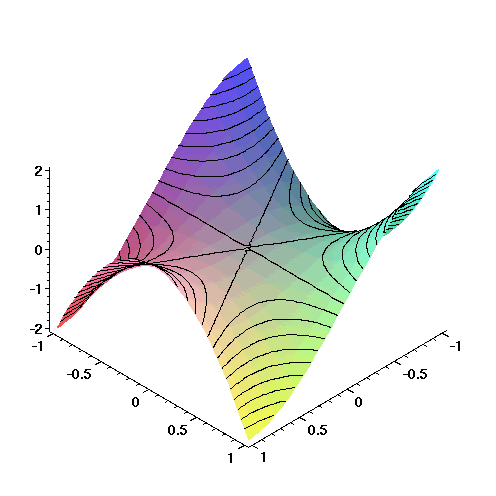
Definovani po castech spojite funkce

Pomoci vetveni.

Syntaxe:

parametr -> if podminka 1 then hodnota 1

elif podminka 2 then hodnota 2

........

elif podminka n then hodnota n
else implicitni hodnota

fi

Definujme nyni funkci, ktera ma hodnotu -1 pro realna cisla mensi jak 1, 0 pro hodnotu x=1 a 1 jinak.

> step:=x-> if x<1 then -1 elif x=1 then 0 else 1 fi;

> step(3/2), step(1), step(1/2);

> plot(step, -1..Pi, discont=true, color=black, scaling=constrained);

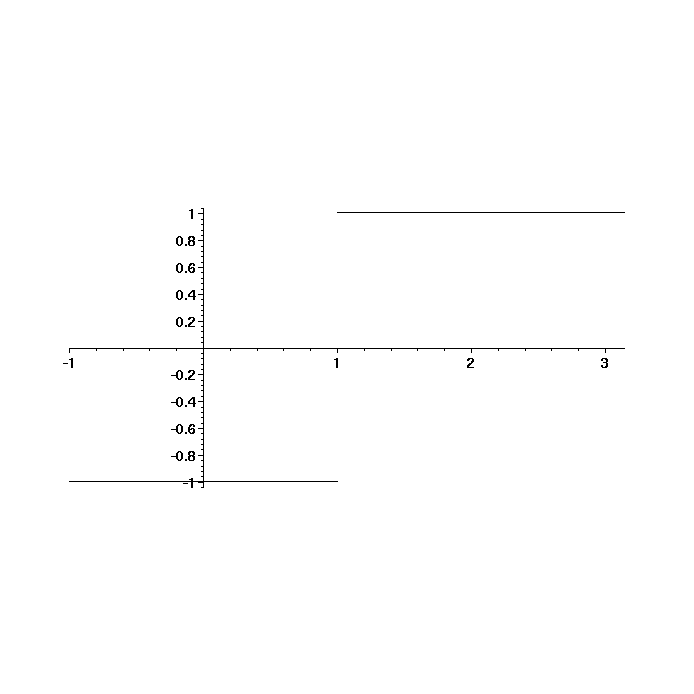
> step(Pi);

Error, (in step) cannot evaluate boolean

Problem je v tom, ze Maple umi porovnavat pouze cisla typu integer, fraction a float.

> step(1.1);

> STEP:=x->piecewise(x<1, -1, x=1, 0, 1);

> STEP(3/2), STEP(1), STEP(1/2), STEP(Pi);

> STEP(u);

> f:=x->piecewise(x<=1, x^2, sin(x));

> D(f);

Definice funkce pomoci Maplovske procedury:

> sgn:=proc(n::integer) (-1)^n end:

> sgn(Pi);

Error, sgn expects its 1st argument, n, to be of type integer, but received Pi

> sgn(4);

Definice procedury ma obecne tuto syntaxi:

proc (posloupnost_parametru)

[ local posloupnost_jmen;]

[ global posloupnost_jmen;]

[ options posloupnost_jmen;]

[ description retezec;]

prikazy

end

U kazdeho parametru muze byt uvedeno, jakeho je typu.
Obecne procedura vraci posledni pocitanou hodnotu.

> y:=proc(x) x^2 end:

> y(x), y(0), y(2);

> whattype(%%);

> restart;

Rekurse:

Rekursivni definici funkce nebo procedury budeme ilustrovat na vypoctu

tzv. Lucasovych cisel Ln, ktere jsou definovany pomoci linerani rekurence:

L(1)=1, L(2)=3, L(n)=L(n-1)+L(n-2) pro n>2

> L:=proc(n::posint)

> if n=1 then 1

> elif n=2 then 3

> else L(n-1)+L(n-2)

> fi

> end:

> L(-6);

Error, L expects its 1st argument, n, to be of type posint, but received -6

> time(L(20));

> readlib(profile):

> profile(L):

> L(6);

> showprofile();

function           depth    calls     time    time%         bytes   bytes%

---------------------------------------------------------------------------

L                      5       15    0.000     0.00         14236   100.00

---------------------------------------------------------------------------

total:                 5       15    0.000     0.00         14236   100.00

> restart;

Pro zefektivneni procedury pouzijeme option remeber, ktera zpusobi zapamatovani

funkcnich hodnot tak, jak jsou pocitany.

> LL:=proc(n::nonnegint) Lucas(n) end:

pri zavolani L je kontrolovan typ argumentu,

pokud je v poradku, vola se rekursivni definice Lukas (timto zamezime opetovnemu testovani argumentu)

> Lucas:=proc(n)

> option remember;

kazda Maplovska procedura je spojena s pametovou tabulkou, ktera se aktivuje pomoci option remember.

Polozky tabulky jsou funkcni hodnoty, indexovane pomoci argumentu, odpovidajicimu volani funkce.

Pokud zavolame Lucas(n), Maple se podiva do tabulky, zda tam neni ulozena odpovidajici

funkcni hodnota. Pokud ne, vyvola se telo procedury a dvojice (n, Lucas(n)) se automaticky ulozi do pametove tabulky. Tim dosahneme, ze kazde cislo je pocitano pouze jednou.

> if n=1 then 1

> elif n=2 then 3

> else Lucas(n-1)+Lucas(n-2)

> fi

> end:

> LL(6);

Pametova tabulka je pristupna jako ctvrty operand procedury.

> op(4, eval(Lucas));

Odstraneni pametove tabulky:

> subsop(4=NULL, eval(Lucas)):

> op(4, eval(Lucas));

> readlib(profile):

> profile(Lucas):

> LL(6);

> showprofile();

function           depth    calls     time    time%         bytes   bytes%

---------------------------------------------------------------------------

Lucas                  5        9    0.000     0.00          8452   100.00

---------------------------------------------------------------------------

total:                 5        9    0.000     0.00          8452   100.00

> time(Lucas(300));

> restart;

> Lucas:=proc(n)

> Lucas(n):=Lucas(n-1)+Lucas(n-2)

> end:

> Lucas(1):=1: Lucas(2):=3:

> op(4, eval(Lucas));

> Lucas(5): op(4, eval(Lucas));

UNAPPLY

Tento zpusob definovani funkce je vyhodny zejmena tehdy, pokud

z nejakeho vyrazu ci formule chceme udelat funkci

> vzorec:=(b^2*x^2*sin(b*x)-2*sin(b*x)+2*b*x*cos(b*x)*a*t)/b^3;

> F:=unapply(vzorec, x, t);

> F(0,1),F(Pi/b,5);

Jine pokusy selhavaji.

> vzorec;

> F:=(x,t)->%;

> F(0,1);

> G:=(x,t)->vzorec;

> F(u,v),G(u,v);

Jinou moznosti je jedine:

> H:=subs(telo=vzorec, (x,t)->telo);

> H(u,v);

Operace s funkcemi.

> f:=x->ln(x)+1; g:=y->exp(y)-1;

> h:=f+g: h(z);

> h:=f*g: h(z);

> h:=f@g: h(z);

> h:=g@f: h(z);

> simplify(%);

> (f@@4)(z); #ekvivalent k f(f(f(f(z))))

> map(x->x^2, a+b+c);

> map(x->x+2, [1,2,3]);