GRAFIKA V MAPLU -- I. CAST
Uvod
| > |
f:=x->exp(-x^2)*sin(Pi*x^3);
|
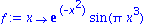
![[Plot]](images/predn7_2.gif)
Prikaz pro nakresleni funkce plot(f, a..b, options), a..b interval na ose x, options jsou nepovinne.
Pri kresleni formule je treba pouzit plot(f(x), x=a..b, options).
![[Plot]](images/predn7_3.gif)
| > |
plot(f, -infinity..infinity);
|
![[Plot]](images/predn7_4.gif)
V tomto pripade Maple transformuje realnou osu na interval (-1,1).
Vice funkci v jednom obrazku:
| > |
plot({f(x), exp(-x^2), -exp(-x^2)}, x=-2..2);
|
![[Plot]](images/predn7_5.gif)
| > |
plot([sin(x), cos(x)], x=0..2*Pi, color=[red, blue], thickness=[2,3], legend=["sin", "cos"]); |
![[Plot]](images/predn7_6.gif)
Pokud chceme omezit rozsah zobrazovanych hodnot na ose y, musime to Maplu sdelit:
| > |
plot(sin(x^2)/x^2, x=-6..6, y=0..1);
|
![[Plot]](images/predn7_7.gif)
Maple voli meritko na obou osach tak, aby obrazek co nejlepe "zaplnil" display. Pokud chceme stejne meritko na osach, pouzijeme volbu scaling=constrained.
| > |
plot(sin(x^2)/x^2, x=-6..6, scaling=constrained, tickmarks=[5,2]);
|
![[Plot]](images/predn7_8.gif)
Nekdy je vymezeni rozsahu zobrazovanych hodnot nutne:
![[Plot]](images/predn7_9.gif)
Warning, the name changecoords has been redefined
| > |
display(%%, view=[-4..4,-10..10]); |
![[Plot]](images/predn7_10.gif)
| > |
plot(tan, -Pi..Pi, -10..10);
|
![[Plot]](images/predn7_11.gif)
Zamezeni "spojovani" nespojitych funkci provedeme pomoci volby discont=true.
| > |
plot(tan(x), x=-Pi..Pi, y=-10..10, discont=true);
|
![[Plot]](images/predn7_12.gif)
| > |
plot(tan(x), x=-Pi..Pi, -10..10, discont=true, xtickmarks=[-3.14=`-p`, -1.57=`-p/2`, 1.57=`p/2`, 3.14=`p`], axesfont=[SYMBOL,12]);
|
![[Plot]](images/predn7_13.gif)
| > |
plot(sin(x), x=0..20, `y(x)`=-0.5..1, xtickmarks=8, ytickmarks=4, title=`Graf funkce sinus`);
|
![[Plot]](images/predn7_14.gif)
| > |
plot(sin(x), x=0..20, `y(x)`=-0.5..1, xtickmarks=[5,10,15,20], ytickmarks=[-0.4,0,1], title=`Graf funkce sinus`); |
![[Plot]](images/predn7_15.gif)
| > |
plot1:=plot(sin, 0..20, -0.5..1, tickmarks=[5,9], title= `Graf funkce sinus`): |
| > |
plot2:=textplot({[4,0.75,`sin(x)`]}, align={ABOVE, RIGHT}): |
Implicitni nastaveni je centrovani horozontalni i vertikalni. Zarovnani menime parametrem align=t, kde t muze byt BELOW,RIGHT,ABOVE a LEFT.
| > |
display({plot1, plot2});
|
![[Plot]](images/predn7_16.gif)
Pro znazornovani dat se pouziva style=point.
| > |
plot(sin, 0..2*Pi, scaling=constrained, style=point);
|
![[Plot]](images/predn7_17.gif)
| > |
plot(sin, 0..2*Pi, scaling=constrained, style=point, symbol=circle);
|
![[Plot]](images/predn7_18.gif)
| > |
plotpoints:=[seq([i, ithprime(i)], i=1..9)];
|
![plotpoints := [[1, 2], [2, 3], [3, 5], [4, 7], [5, 11], [6, 13], [7, 17], [8, 19], [9, 23]]](images/predn7_19.gif)
| > |
plot(plotpoints, style=point, symbol=box);
|
![[Plot]](images/predn7_20.gif)
![[Plot]](images/predn7_21.gif)
| > |
plots[polygonplot]([[3,-2],[7,-2],[5,5]],color=grey,axes=framed);
|
![[Plot]](images/predn7_22.gif)
Styl a tloustka car
| > |
for i from 0 to 15 do
thick[i]:=plot(i, x=0..1, thickness=i):
od:
|
| > |
display(convert(thick, set), axes=box, tickmarks=[0,15], title=`thickness option: [0,1,...,15]` );
|
![[Plot]](images/predn7_23.gif)
| > |
for i from 1 to 4 do
line[i]:=plot(i, x=0..1, linestyle=i):
od:
|
| > |
display(convert(line, set), axes=box, tickmarks=[1,4], title=`linestyle option: [1,2,3,4]`);
|
![[Plot]](images/predn7_24.gif)
| > |
interactive(sin(x), x); |
![[Plot]](images/predn7_25.gif)
Struktura dvoj-dimenzionalni grafiky
Vytvareni obrazku probiha ve dvou fazich:
1) Jsou spocitany funkcni hodnoty v referencnich bodech a tyto jsou ulozeny do objektu datoveho typu PLOT.
2) Objekt je vykreslen na obrazovce.
| > |
PLOT(CURVES([[1,1],[2,2], [3,1], [1,1]]), AXESSTYLE(NONE), SCALING(CONSTRAINED));
|
![[Plot]](images/predn7_26.gif)
| > |
P:=plot([[1,1], [2,2], [3,1], [1,1]], axes=none, scaling=constrained);
|
![P := INTERFACE_PLOT(CURVES([[1., 1.], [2., 2.], [3., 1.], [1., 1.]], COLOUR(RGB, 1.0, 0., 0.)), AXESLABELS(](images/predn7_27.gif)
![P := INTERFACE_PLOT(CURVES([[1., 1.], [2., 2.], [3., 1.], [1., 1.]], COLOUR(RGB, 1.0, 0., 0.)), AXESLABELS(](images/predn7_28.gif)
![[Plot]](images/predn7_29.gif)
| > |
f:=x->sqrt(2)-sqrt(2*sqrt(x)):
|
| > |
P:=plot(f(x), x=0..1, y=0..sqrt(2));
|
![P := INTERFACE_PLOT(CURVES([[0., 1.41421356237309515], [0.681161067708333304e-3, 1.18574447219701806], [0.136232213541666661e-2, 1.14251649477750617], [0.204348320312499991e-2, 1.11353133002946070], [...](images/predn7_30.gif)
![P := INTERFACE_PLOT(CURVES([[0., 1.41421356237309515], [0.681161067708333304e-3, 1.18574447219701806], [0.136232213541666661e-2, 1.14251649477750617], [0.204348320312499991e-2, 1.11353133002946070], [...](images/predn7_31.gif)
![P := INTERFACE_PLOT(CURVES([[0., 1.41421356237309515], [0.681161067708333304e-3, 1.18574447219701806], [0.136232213541666661e-2, 1.14251649477750617], [0.204348320312499991e-2, 1.11353133002946070], [...](images/predn7_32.gif)
![P := INTERFACE_PLOT(CURVES([[0., 1.41421356237309515], [0.681161067708333304e-3, 1.18574447219701806], [0.136232213541666661e-2, 1.14251649477750617], [0.204348320312499991e-2, 1.11353133002946070], [...](images/predn7_33.gif)
![P := INTERFACE_PLOT(CURVES([[0., 1.41421356237309515], [0.681161067708333304e-3, 1.18574447219701806], [0.136232213541666661e-2, 1.14251649477750617], [0.204348320312499991e-2, 1.11353133002946070], [...](images/predn7_34.gif)
![P := INTERFACE_PLOT(CURVES([[0., 1.41421356237309515], [0.681161067708333304e-3, 1.18574447219701806], [0.136232213541666661e-2, 1.14251649477750617], [0.204348320312499991e-2, 1.11353133002946070], [...](images/predn7_35.gif)
![P := INTERFACE_PLOT(CURVES([[0., 1.41421356237309515], [0.681161067708333304e-3, 1.18574447219701806], [0.136232213541666661e-2, 1.14251649477750617], [0.204348320312499991e-2, 1.11353133002946070], [...](images/predn7_36.gif)
![P := INTERFACE_PLOT(CURVES([[0., 1.41421356237309515], [0.681161067708333304e-3, 1.18574447219701806], [0.136232213541666661e-2, 1.14251649477750617], [0.204348320312499991e-2, 1.11353133002946070], [...](images/predn7_37.gif)
![P := INTERFACE_PLOT(CURVES([[0., 1.41421356237309515], [0.681161067708333304e-3, 1.18574447219701806], [0.136232213541666661e-2, 1.14251649477750617], [0.204348320312499991e-2, 1.11353133002946070], [...](images/predn7_38.gif)
![P := INTERFACE_PLOT(CURVES([[0., 1.41421356237309515], [0.681161067708333304e-3, 1.18574447219701806], [0.136232213541666661e-2, 1.14251649477750617], [0.204348320312499991e-2, 1.11353133002946070], [...](images/predn7_39.gif)
![P := INTERFACE_PLOT(CURVES([[0., 1.41421356237309515], [0.681161067708333304e-3, 1.18574447219701806], [0.136232213541666661e-2, 1.14251649477750617], [0.204348320312499991e-2, 1.11353133002946070], [...](images/predn7_40.gif)
![P := INTERFACE_PLOT(CURVES([[0., 1.41421356237309515], [0.681161067708333304e-3, 1.18574447219701806], [0.136232213541666661e-2, 1.14251649477750617], [0.204348320312499991e-2, 1.11353133002946070], [...](images/predn7_41.gif)
![P := INTERFACE_PLOT(CURVES([[0., 1.41421356237309515], [0.681161067708333304e-3, 1.18574447219701806], [0.136232213541666661e-2, 1.14251649477750617], [0.204348320312499991e-2, 1.11353133002946070], [...](images/predn7_42.gif)
![P := INTERFACE_PLOT(CURVES([[0., 1.41421356237309515], [0.681161067708333304e-3, 1.18574447219701806], [0.136232213541666661e-2, 1.14251649477750617], [0.204348320312499991e-2, 1.11353133002946070], [...](images/predn7_43.gif)
![P := INTERFACE_PLOT(CURVES([[0., 1.41421356237309515], [0.681161067708333304e-3, 1.18574447219701806], [0.136232213541666661e-2, 1.14251649477750617], [0.204348320312499991e-2, 1.11353133002946070], [...](images/predn7_44.gif)
![P := INTERFACE_PLOT(CURVES([[0., 1.41421356237309515], [0.681161067708333304e-3, 1.18574447219701806], [0.136232213541666661e-2, 1.14251649477750617], [0.204348320312499991e-2, 1.11353133002946070], [...](images/predn7_45.gif)
![P := INTERFACE_PLOT(CURVES([[0., 1.41421356237309515], [0.681161067708333304e-3, 1.18574447219701806], [0.136232213541666661e-2, 1.14251649477750617], [0.204348320312499991e-2, 1.11353133002946070], [...](images/predn7_46.gif)
![P := INTERFACE_PLOT(CURVES([[0., 1.41421356237309515], [0.681161067708333304e-3, 1.18574447219701806], [0.136232213541666661e-2, 1.14251649477750617], [0.204348320312499991e-2, 1.11353133002946070], [...](images/predn7_47.gif)
![P := INTERFACE_PLOT(CURVES([[0., 1.41421356237309515], [0.681161067708333304e-3, 1.18574447219701806], [0.136232213541666661e-2, 1.14251649477750617], [0.204348320312499991e-2, 1.11353133002946070], [...](images/predn7_48.gif)
![P := INTERFACE_PLOT(CURVES([[0., 1.41421356237309515], [0.681161067708333304e-3, 1.18574447219701806], [0.136232213541666661e-2, 1.14251649477750617], [0.204348320312499991e-2, 1.11353133002946070], [...](images/predn7_49.gif)
Nejdrive se vyhodnoti prvni argument prikazu plot (popisuje zadanou funkci), dale jsou vybrany equidistantni body ze zadaneho intervalu (implicitne 49 bodu) a numericky jsou v techto bodech spocteny funkcni hodnoty. Dale se maple diva na tyto body, jako by byly spojeny useckami a kontroluje, jestli mezi nekterymi useckami neni prilis velky uhel. Pokud ano, prida do teto oblasti dalsi referencni body. Maximalni pocet referencnich bodu je urcovan promennou resolution, jejiz implicitni hodnota je 200. Tedy pocet referencnich bodu je cele cislo z intervalu [49,200].
Pomoci funkce replot z balicku plots muzeme zvetsovat ci zmensovat drive nakresleny obrazek a ilustrovat vyse uvedenou skutecnost.
| > |
plots[replot] (P, x=0..0.01, y=1..sqrt(2));
|
![[Plot]](images/predn7_50.gif)
| > |
plot(f(x), x=0..1, y=0..sqrt(2)):
|
`plot/adaptive:`, `evalhf succeeded`
`plot/adaptive:`, `produced `, 59., ` output segments`
`plot/adaptive:`, `using `, 59., ` function evaluations`
| > |
plot(f(x), x=0..1, y=0..sqrt(2), adaptive=false):
|
`plot/adaptive:`, `evalhf succeeded`
`plot/adaptive:`, `produced `, 49., ` output segments`
`plot/adaptive:`, `using `, 49., ` function evaluations`
| > |
plot(x^2, x=0..1, sample=[0,1/2,1], adaptive=true);
|
![[Plot]](images/predn7_51.gif)
| > |
plot(x^2, x=0..1, sample=[0,1/2,1], adaptive=false);
|
![[Plot]](images/predn7_52.gif)
| > |
plot(x/(1-cos(5*x)), x=-5..5, -5..5);
|
![[Plot]](images/predn7_53.gif)
| > |
plot(x/(1-cos(5*x)), x=-5..5, -5..5, numpoints=200);
|
![[Plot]](images/predn7_54.gif)
| > |
plot(x+sin(2*Pi*x), x=0..49);
|
![[Plot]](images/predn7_55.gif)
| > |
plot(x+sin(2*Pi*x), x=0..49, numpoints=200);
|
![[Plot]](images/predn7_56.gif)
Pokud chceme nejakou option zmenit pro celou session, musime jeji hodnotu nastavit pomoci procedury setoptions.
| > |
setoptions(scaling=constrained); |
Specialni dvoj-dimenzionalni obrazky
Funkce dana parametricky:
syntaxe: plot([f(t), g(t), t=a..b], options)
| > |
plot([t*cos(2*Pi*t), t*sin(2*Pi*t), t=0..10], numpoints=500, scaling=constrained, axes=none);
|
![[Plot]](images/predn7_58.gif)
| > |
plot([cos, sin, 0..2*Pi], scaling=constrained);
|
![[Plot]](images/predn7_59.gif)
Krivka v polarnich souradnicich:
polarplot(r-expr,angle=range)
| > |
plots[polarplot](sin(3*theta), theta=0..2*Pi);
|
![[Plot]](images/predn7_60.gif)
polarplot([r-expr, angle-expr, parameter=range)
| > |
plots[polarplot]([sin(t), cos(t), t=0..2*Pi]);
|
![[Plot]](images/predn7_61.gif)
| > |
plot([sin(t)/t, t, t=-6*Pi..6*Pi], coords=polar, numpoints=250);
|
![[Plot]](images/predn7_62.gif)
Krivka dana implicitne rovnici
| > |
implicitplot(x^3+y^3-5*x*y+1/5=0, x=-3..3, y=-3..3, grid=[50,50]);
|
![[Plot]](images/predn7_63.gif)
Maple pracuje se zadanou rovnici jako s funkci dvou promennych a generuje vrstevnici teto funkce na hladine z=0 (rez rovinou z=0).
Nevyhodou teto metody je, ze ziskane obrazky mohou byt "kostrbate" v okoli singularit a mistech, kde krivka protina sebe samu.
| > |
implicitplot(2*x^4+y^4-3*x^2*y-2*y^3+y^2, x=-5/2..5/2, y=-5/2..5/2,scaling=constrained);
|
![[Plot]](images/predn7_64.gif)
| > |
v:=algcurves[parametrization](2*x^4+y^4-3*x^2*y-2*y^3+y^2,x,y,t); |
![v := [(18-15*t-1548*t^2-6883*t^3-8470*t^4)/(43257*t^4+26696*t^3+5056*t^2+336*t+18), (36+516*t+2689*t^2+6020*t^3+4900*t^4)/(43257*t^4+26696*t^3+5056*t^2+336*t+18)]](images/predn7_65.gif)
| > |
plot([op(v), t=-infinity..infinity], scaling=constrained); |
![[Plot]](images/predn7_66.gif)
Prokladani krivek (linearni regrese, metoda nejmensich ctvercu) - pouzijeme balik statistic:
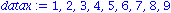
| > |
datay:=seq(ithprime(i), i=1..9);
|
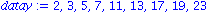
| > |
with(stats); Digits:=5;
|
![[anova, describe, fit, importdata, random, statevalf, statplots, transform]](images/predn7_69.gif)
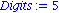
| > |
aproximace:=fit[leastsquare[[x,y], y=a*x+b, {a,b}]]([[datax],[datay]]);
|
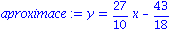
| > |
pair:=(x,y)->[x,y];
plotpoints:=zip(pair, [datax],[datay]);
|
![pair := proc (x, y) options operator, arrow; [x, y] end proc](images/predn7_72.gif)
![plotpoints := [[1, 2], [2, 3], [3, 5], [4, 7], [5, 11], [6, 13], [7, 17], [8, 19], [9, 23]]](images/predn7_73.gif)
| > |
plot1:=plot(plotpoints, style=point): |
| > |
plot2:=plot(rhs(aproximace), x=0..10): |
| > |
plots[display]({plot1,plot2});
|
![[Plot]](images/predn7_74.gif)
Nasledujici obrazek ukazuje oblast, vyhovujici nerovnicim x+y<5, 0<x, x<=4.
| > |
plots[inequal]({x+y<5, 0<x, x<=4}, x=-1..5, y=-10..10, optionsexcluded=(color=yellow));
|
![[Plot]](images/predn7_75.gif)
Ukladani grafiky
Ulozeni obrazku do postscriptu:
| > |
plot(sin(x), x=-Pi..Pi);
|
![[Plot]](images/predn7_76.gif)
Nejprve prikazem
| > |
plotsetup(cps, plotoutput="sin.eps", plotoptions= "portrait,noborder,leftmargin=0,bottommargin=0"); |
Maplu sdelime, ze ma graficky vystup ukladat do postscriptoveho souboru sin.eps. Pote vygenerujeme obrazek, jehoz vystup se neobjevi na obrazovce, ale ulozi do souboru sin.eps v aktulanim adresari.
Zamezit kresleni ramecku kolem obrazku muzeme pouzitim doplnujiciho parametru plotoptions=noborder. Vystup grafiky zpet do zapisniku vratime prikazem:
![]()
![[Plot]](images/predn7_2.gif)
![[Plot]](images/predn7_3.gif)
![[Plot]](images/predn7_4.gif)
![[Plot]](images/predn7_5.gif)
![[Plot]](images/predn7_6.gif)
![[Plot]](images/predn7_7.gif)
![[Plot]](images/predn7_8.gif)
![[Plot]](images/predn7_9.gif)
![[Plot]](images/predn7_10.gif)
![[Plot]](images/predn7_11.gif)
![[Plot]](images/predn7_12.gif)
![[Plot]](images/predn7_13.gif)
![[Plot]](images/predn7_14.gif)
![[Plot]](images/predn7_15.gif)
![[Plot]](images/predn7_16.gif)
![[Plot]](images/predn7_17.gif)
![[Plot]](images/predn7_18.gif)
![]()
![[Plot]](images/predn7_20.gif)
![[Plot]](images/predn7_21.gif)
![[Plot]](images/predn7_22.gif)
![[Plot]](images/predn7_23.gif)
![[Plot]](images/predn7_24.gif)
![[Plot]](images/predn7_25.gif)
![[Plot]](images/predn7_26.gif)
![[Plot]](images/predn7_29.gif)
![[Plot]](images/predn7_50.gif)
![[Plot]](images/predn7_51.gif)
![[Plot]](images/predn7_52.gif)
![[Plot]](images/predn7_53.gif)
![[Plot]](images/predn7_54.gif)
![[Plot]](images/predn7_55.gif)
![[Plot]](images/predn7_56.gif)
![[Plot]](images/predn7_58.gif)
![[Plot]](images/predn7_59.gif)
![[Plot]](images/predn7_60.gif)
![[Plot]](images/predn7_61.gif)
![[Plot]](images/predn7_62.gif)
![[Plot]](images/predn7_63.gif)
![[Plot]](images/predn7_64.gif)
![v := [(18-15*t-1548*t^2-6883*t^3-8470*t^4)/(43257*t^4+26696*t^3+5056*t^2+336*t+18), (36+516*t+2689*t^2+6020*t^3+4900*t^4)/(43257*t^4+26696*t^3+5056*t^2+336*t+18)]](images/predn7_65.gif)
![[Plot]](images/predn7_66.gif)
![[Plot]](images/predn7_74.gif)
![[Plot]](images/predn7_75.gif)
![[Plot]](images/predn7_76.gif)