Prirazeni a vyhodnoceni

>

restart;

CAS systemy jsou schopny pracovat s formulemi a resit ulohy, ve kterych se vyskytuji nezname a parametry.

>	solve(a*x^2+b*x+c,x);

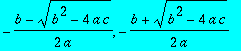
Zda a,b a c jsou koeficienty a x je neznama. Toto pouziti "volnych promennych", ktere nemaji prirazenu zadnou hodnotu, krome jejich vlastniho jmena, je charakteristicke pro symbolicke systemy.

Promennym prirazujeme hodnoty pomoci operatoru :=.

jmeno:=vyraz;

>	pol:=9*x^3-37*x^2+47*x-19;

Urcime koreny tohoto polynomu.

>	roots(pol);

Dosazeni jednoho z korenu do polynomu:

>	subs(x=19/9,pol);

V promenne pol je ulozena hodnota 9*x^3-..... Kdykoliv v Maplu zadame promennou pol, Maple pracuje s jeji hodnotou. Tomu rikame vyhodnoceni.

Promenna x stale nema jinou hodnotu (krome sveho jemna), zustava nevyhodnocena.

Prikazem subs jsme v promenne pol nahradili x pomoci 19/9, x zustava nezmeneno. To same plati pro promennou pol.

>

x;

>

pol;

>

x:=19/9;

>

x;

>

pol;

Maple nejdrive vyhodnoti promennou pol do do 9*x^3-...., potom vyhodnoti kazde x do 19/9 a nakonec provede zjednoduseni.

>

x+1;

>	x:=neznama;

>

pol;

>	neznama:=7;

>

x;

>

pol;

Maple vyhodnocuje tak hluboko, jak je to v danem stavu systemu mozne. Toto obecne pravidlo se nazyva uplne vyhodnoceni.

Vyjimky z pravidla uplneho vyhodnocovani:
 vyrazy, ktere jsou uzavreny v pravych uvozovkach se nevyhodnocuji

>

x;

>

'x';

Uzavreni do pravych uvozovek nezamezuje automaticke zjednoduseni:

>	'p+q-i-p+3*q';

Pokud do pravych uvozovek (apostrofu) uzavreme jednoduchou promennou, je vysledkem jmeno teto promenne. Tohoto muzeme vyuzit k zpetnemu vyhodnoceni promenne pouze do jmena.

>

x:='x';

Jmena nalevo od prirazovaciho operatoru := se nevyhodnocuji

>

x;

>

x:=1;

>

x:=7;

>	i:=1; A[i]:=2; A[i]:=3;

Vidime, ze index u indexovane promenne je vyhodnocovan, ale indexovana promenna uz dale vyhodnocovana neni (v tretim prikazu je leva strana A[i]  vyhodnocena do A[1] , ale to uz dale neni vyhodnoceno do 2.

Zpetne vyhodnoceni promenne pouze do jmena s vyuzitim pravych uvozovek nefunguje u indexovanych promennych.

>	A[i]:='A[i]';

>

A[i];

Error, too many levels of recursion

>

x:='x';

>

x:=x+1;

Error, recursive assignment

K odstraneni prirazeni (ukazatele) u indexovanych promennych muzeme pouzit prikaz evaln() .

>	A[i]:=evaln(A[i]); A[i];

argument procedury evaln se nevyhodnocuje

tj. stejneho efektu jako prikazem x:='x'; dosahneme i prikazem x:=evaln(x);

>

evaln(x);

>

restart;

>	p:=q; r:=q*s;

>

anames();

Vypisuje vsechny promenne s prirazenou hodnotou.

>	anames('integer');

>	anames('user');

>

unames():

>	nops({%});

Vypisuje vsechny "volne" promenne.

>	select(s->length(s)=1, {unames()});

argument procedury assigned se nevyhodnocuje

>	assigned(r);

Urcuje, zda je promenna "volna" nebo "vazana".

>	assigned(q);

Procedura assign(name, expression) ma stejny efekt jako name:=expression s vyjimkou toho, ze prvni argument procedury assig je plne vyhodnocen, zatimco leva strana prirazeni pomoci := neni vyhodnocena.

>

restart;

>

x:=1;

>

x:=2;

>	assign(x,3);

Error, (in assign) invalid arguments

Proceduru assign pouzivame pro prirazeni hodnot promennym pri reseni systemu rovnic.

>

restart;

>	eqns:={x+y=a, b*x-1/3*y=c};

>	vars:={x,y}:

>	sols:=solve(eqns,vars);

>

x;y;

>	assign(sols);

>

x, y;

Proceduru (prikaz) unassign muzeme pouzit pro odstraneni hodnot u vice promennych naraz.

Vsimneneme si ale opomenuti pravidla uplneho vyhodnocovani:

>	unassign(x,y): x,y;

Error, (in unassign) cannot unassign `(3*c+a)/(3*b+1)' (argument must be assignable)

>	unassign('x','y'): x,y;

>

restart;

Uplne vyhodnocovani nam dale priblizi nasledujici posloupnost prikazu:

>	a:=b; b:=c; c:=3;

Pokud ted zadame a;, jaky bude vysledek?

>

a;

Pro zjisteni interni datove reprezentace pouzijeme prikaz eval .

>	eval(a,1);

>

eval(a);

>	eval(b,1);

>	eval(c,1);

>	eval(a,2);

>	eval(a,3);

Prikaz eval bez doplnujiciho parametru provadi uplne vyhodnoceni argumentu, volitelny parametr urcuje uroven vyhodnoceni.

>

c:=5;

>

a;

>	eval(a,1);

>

a:=4;

>	a;eval(a,1);

>

restart;

>	x:=y: y:=7:

>	eval(x,1); x;

>

x:=x:

>

y:=9:

Jaka hodnota je ted ulozena v promenne x?

>

x;

Nejjistejsi zpusob, jak zamezit vyhodnocovani, je uzavrit argument do apostrofu (' ');
Pr:

>

restart;

>

podil:=0;

>	rem(x^3+x+1,x^2+x+1,x,'podil');

>

podil;

Co se stane, pokud zapomeneme apostrofy v predchazejicim prikazu?

>

podil:=0;

>	rem(x^3+x+1,x^2+x+1,x,podil);

Error, (in rem) illegal use of a formal parameter

>

podil:=x;

>	rem(x^3+x+1,x^2+x+1,x,podil);

>	eval(podil,1), eval(podil,2);

>

podil;

Error, too many levels of recursion

>

i:=0;

>	sum(ithprime(i), i=1..5);

Error, (in ithprime) argument must be of type posint

>	sum(ithprime('i'), i=1..5);

Error, (in sum) summation variable previously assigned, second argument evaluates to 0 = 1 .. 5

>	sum(ithprime('i'), 'i'=1..5);

prikaz seq  nevyhodnocuje svoje argumenty, vsimnete si rozdilneho chovani prikazu sum

>

i:=2;

>	seq(i^2, i=1..5);

>

i;

Datove struktury array, table, matrix a proc maji pro vyhodnocovani specialni pravidlo: last name evaluation.

>

restart;

>

x:=y;

>

y:=z;

>	z:=array([[1,2], [3,4]]);

>

x;

Maple vyhodnoti x do y, y do z a ukonci vyhodnocovani, protoze posledni promenna z by se vyhodnotila do jedne ze specialnich datovych struktur.

Uplneho vyhodnoceni dosahneme pomoci prikazu eval.

>

eval(x);

Lokalni promenne uvnitr procedur se vyhodnocuji pouze o jednu uroven. Pokud chceme dosahnout uplneho vyhodnoceni, musime pouzit funkce eval .